Photo Collage Generation Using Genetic Algorithms

11 June 2025 // Marcus Cedergren

Photo Collage Generation Using Genetic Algorithms

This post explores an automated approach to creating high-quality photo collages from large image collections, a journey that began out of frustration with existing tools. The solutions I found, whether manual or automated, often created repetitive patterns, ugly image overlaps, and offered only a fixed set of layouts. This led me to explore a new approach, leveraging a Genetic Algorithm (GA), to efficiently generate large collage layouts. I’ll present an overview of the algorithm and a custom implementation written in Kotlin.

The journey began when I tried to arrange a few hundred photos in an image editing program. This quickly proved to be an endless, tedious task, so I rather quickly started experimenting with scripting a combination of ImageMagick plugins, aiming to automate the process. Although this kind of worked, the results were far from ideal: repetitive patterns, ugly image overlaps, and noticeable gaps between pictures. I also explored various commercial alternatives, but none seemed capable of handling hundreds of images with satisfactory results. Almost all also relied on rigid, fixed layouts that frequently cropped images to fit predefined slots – a limitation I absolutely wanted to avoid. My goal was to just beeing able to select a directory of images and get a good result with minimal effort.

It was during this search for a better solution that I discovered a promising approach outlined in a paper by Jian Fan, which proposed using a genetic algorithm for collage creation. Although I had a basic conceptual understanding of genetic algorithms, I had never applied them to an actual practical problem. This felt like the perfect learning opportunity!

Let’s first briefly delve into what genetic algorithms are and how they function. Then, we’ll connect this theory to the rather complex challenge of generating effective photo collage layouts, and specifically how a GA can provide an elegant solution. Finally, we’ll detail a custom implementation of the algorithm that builds upon Fan’s original algorithm, incorporating additional enhancements such as a fitness metric for improved centering of featured images.

So, What are Genetic Algorithms?

Genetic algorithms (GAs) are a class of optimization algorithms inspired by the process of natural selection. They are particularly well-suited for complex optimization problems characterized by vast search spaces or non-linear relationships, where traditional deterministic methods often struggle to find optimal (or even good) solutions efficiently. GAs excel at discovering “good enough” solutions for real-world problems that might lack a precise mathematical model. Their beauty lies in their simplicity and general applicability – the core requirements are merely defining a robust fitness function and appropriate genetic operators tailored to your specific problem domain.

The underlying principle of genetic algorithms is to mimic the evolutionary process through a series of iterative steps:

• Create Initial Population: Begin by generating a randomized set of potential solutions, known as “individuals.”
• Evaluate Fitness: Assess the quality (fitness) of each individual in the current population against predefined criteria.
• Selection: Choose the fittest individuals from the current generation to serve as “parents” for the next. This biases the population towards better solutions over time.
• Crossover: Combine genetic material (parts of solutions) from selected parents to create new “offspring.” This introduces new variations.
• Mutation: Introduce small, random changes to the offspring’s genetic material. This helps maintain population diversity and prevents the algorithm from getting stuck in local optima.

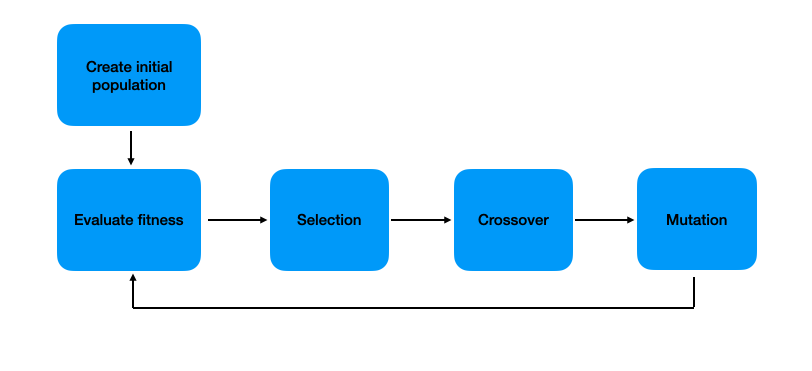
This cyclical process is repeated for multiple generations. Over time, just as natural selection leads to better-adapted organisms, genetic algorithms tend to produce increasingly better solutions to the problem at hand.

The Collage Layout Problem: Why GAs are a Perfect Fit

Creating an appealing image collage involves arranging multiple images on a rectangular canvas, seemingly simple at first glance. However, the problem quickly escalates in complexity when you introduce real-world constraints:

• Images can have wildly different sizes and aspect ratios.
• All images must maintain their original proportions (no cropping or arbitrary rotation).
• There must be absolutely no overlap between images.
• The final collage image should be filled efficiently, minimizing undesirable gaps.
• One might need to have a specific output size (e.g when ordering from a printshop, you will have a limited selection of dimensions to choose from)

As Jian Fan states in his paper, this quickly becomes an

“NP-complete combinatorial optimization problem. An exhaustive search is impractical even for a modest number of photos.”

This inherent complexity, combined with the need for a “good enough” solution rather than a computationally expensive perfect one, makes it an ideal candidate for a genetic algorithm approach.

1. Representation (Individuals)

In the algorithm, each individual in the population represents a complete collage layout of all source images. The layout is structured as a binary tree consisting of two types of nodes:

• Internal nodes (implementead as a LayoutNode): These represent divisions of the canvas, which can be either horizontal (left / right) or vertical (top / bottom)
• Leaf nodes (implemented as an ImageNode): These represent the actual images placed within the collage.

Such a tree, where each node has either zero or two child nodes, is commonly known as a “full binary tree”. This structure inherently helps manage the spatial relationships between images. Below is a debug text rendering using the BinaryTreePrinter the for a 10 image collage solution from a testcase in the project that illustrates the tree structure:

Binary Tree: 
   V: 1823x1080 
   ├──H: 1103x1080 
   │  ├──V: 1103x815 
   │  │  ├──H: 288x815 
   │  │  │  ├──H: 288x599 
   │  │  │  │  ├──Image-7 Size: 288x216 ≈ 36% of 800x600 (weight: 1) @1,333
   │  │  │  │  └──Image-8 Size: 288x384 ≈ 20% of 1440x1920 (weight: 1) @0,750
   │  │  │  └──Image-0 Size: 288x216 ≈ 9% of 3072x2304 (weight: 1) @1,333
   │  │  └──Image-3 Size: 815x815 ≈ 68% of 1200x1200 (weight: 10) @1,000
   │  └──V: 1103x265 
   │     ├──V: 551x265 
   │     │  ├──Image-4 Size: 353x265 ≈ 22% of 1600x1200 (weight: 1) @1,333
   │     │  └──Image-9 Size: 198x265 ≈ 12% of 1712x2288 (weight: 1) @0,748
   │     └──V: 551x265 
   │        ├──Image-5 Size: 198x265 ≈ 12% of 1712x2288 (weight: 1) @0,748
   │        └──Image-6 Size: 353x265 ≈ 44% of 800x600 (weight: 1) @1,333
   └──H: 720x1080 
      ├──Image-1 Size: 720x540 ≈ 28% of 2592x1944 (weight: 3) @1,333
      └──Image-2 Size: 720x540 ≈ 23% of 3072x2304 (weight: 3) @1,333

2. Initialization

The initial population is created by generating a diverse set of random individuals. For each individual:

• A binary tree is constructed with random horizontal and vertical divisions, defining the potential slots for images.
• Images are then randomly assigned to the leaf nodes of the tree (the slots).

Finally, the dimensions and positions of all nodes in the tree are calculated based on these assignments and divisions.

This process ensures a highly varied starting population. While these random layouts will be far from optimal – often exhibiting many gaps and images downsized to minuscule sizes (e.g., 8x8 pixels) – they serve as the raw material for evolution. The only strict requirement is that they adhere to the basic constraints of a valid, non-overlapping layout.

3. Fitness Function: Guiding the Evolution

The fitness (or score) of an individual is the crucial metric that determines how “good” a particular collage layout is. Our goal is to minimize this score, so a lower fitness indicates a better layout. The fitness score is determined by combining three main factors:

1. Canvas Coverage: This measures how effectively the images fill the available space of the canvas, aiming to minimize any wasted “gap” area.
2. Relative Area Coverage: This assesses how closely the sizes of the placed images match their desired proportions or target sizes, preventing images from being excessively scaled down.
3. Featured Image Centering: A new metric added in my implementation that scores how close to the the center of the canvas each “featured” image is positioned.

These factors are combined using configurable weights, allowing us to fine-tune the importance of each scoring component relative to the others. For example, by increasing the weight of the “centered feature” factor, the algorithm will prioritize placing featured images near the collage’s center. It’s crucial to remember that increasing all weights simultaneously is pointless, as they are competing metrics.

4. Selection: Choosing the Best Parents

The selection process determines which individuals from a generation will become parents for the next. In this implementation, I use a simple, elitistic selection strategy: only individuals from the top 25% of the scored population are chosen. This ensures that only the most promising layouts contribute to the next generation, driving the evolution towards better solutions.

5. Crossover: Blending Solutions

The crossover operation combines genetic material from two parent layouts to create a new offspring layout, introducing beneficial traits from both. In this implementation, this is achieved by:

1. Identifying a corresponding subtree in each parent layout that contains the same number of image nodes.
2. Swapping the slicing directions (horizontal ‘H’ or vertical ‘V’) of two selected nodes within these subtrees. This subtly alters how parts of the collage are divided.
3. Using a clone of the parent with the better overall fitness score as the primary basis for the offspring, then applying the swapped slicing directions.

This approach effectively preserves much of the parents’ successful structural elements while introducing variation, leading to novel, potentially improved layouts.

6. Mutation: Introducing Diversity and Escaping Local Maxima

Mutation introduces random changes to the offspring’s genetic material, crucial for maintaining diversity within the population and enabling the algorithm to explore new regions of the solution space. This helps prevent premature convergence and avoids getting trapped in “local maxima” – suboptimal solutions that the algorithm might otherwise settle for. In this implementation, mutation randomly performs one of two operations:

• Swaps the slicing direction (H or V) of two random LayoutNodes within the tree, or
• Swaps the source images assigned to two random ImageNodes.

These random perturbations allow the algorithm to discover novel combinations and push beyond incremental improvements.

7. Evolution: The Iterative Improvement Loop

The entire evolutionary process runs for a specified number of generations. In each generation:

1. New offspring are created through the selection, crossover, and mutation steps.
2. The fitness of these newly generated individuals is evaluated.
3. The algorithm continuously keeps track of the single best solution found across all generations so far.

To illustrate how the solution progresses, heres are two images of a collage created using the sample images included in the repository.

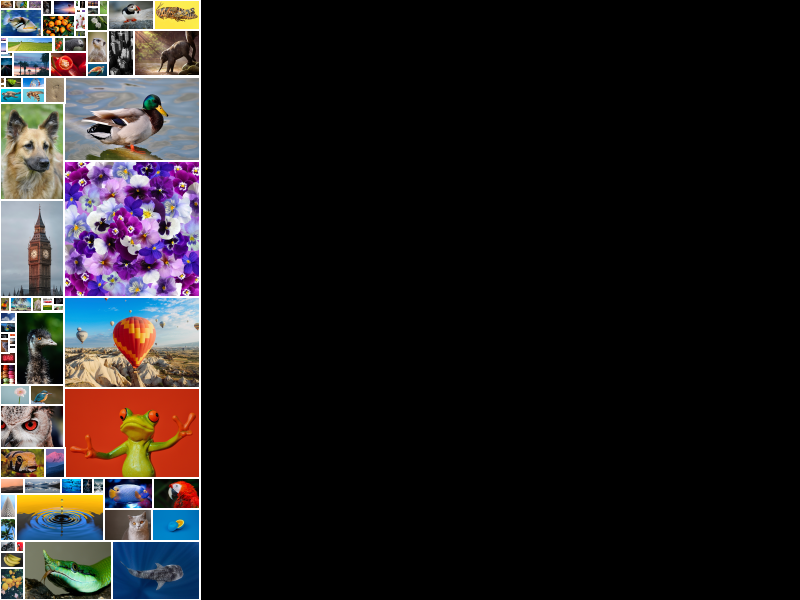
The 800 x 600 output above exemplifies the typical state of the genetic algorithm’s initial population (population: 1, generation: 1) - essentially what the algorithm’s randomized V/H slicing logic will create without any iterative evolutionary guidance. None of the desired metrics is reflected in the output.

Same example but after 500 generations (population: 1000, generation: 500, with an image of a meerkat as a featured image with some boosted centering)

Tuning Your Collage

For the best collage results, I recommend experimenting with the parameters, particularly the ones described here. Different image sets often benefit from specific tuning to achieve optimal aesthetics.

• Target dimensions: Define the overall width and height of the final output collage.
• Population size: Larger populations can explore more solutions and potentially yield better results, but at the cost of increased processing time and memory usage per generation.
• Number of generations: More generations allow the algorithm more time to optimize and refine layouts.
• Mutation probability: Controls the frequency of random changes, influencing the balance between exploration and exploitation.
• Weight factors: As discussed in the fitness function, adjusting these weights is key to tweaking the final results. For example, a higher weight for “Featured Image Centering” will prioritize placing selected images closer to the middle of the collage, with the cost of slightly decreasing the importance of the other score metrics.

By carefully experimenting with these parameters, you can fine-tune the genetic algorithm to produce collages that meet your specific aesthetic and functional requirements. I had a lot of fun creating this - I hope it may be useful for others!

References

1. Fan, J. (2012). Photo Layout with a Fast Evaluation Method and Genetic Algorithm, IEEE International Conference on Multimedia and Expo Workshops, Melbourne, VIC, Australia, pp. 308-313.
2. Collage Solver Project: GitHub Repository